TreeMeasurementApp/docs/How.md

How does it work?

The underlying mathematical principal used is trigonometry. The used formulas assume, that a reference height is known. This could be a stick of a known length leaned against the tree as optical marker, or an actual marker on the tree at a known height. Given that known height, the height of the entire tree can be calculated without actually knowing the distance to the tree.

The implementation was inspired by the formulas and explanations given at the AWF-Wiki of University of Göttingen. They present the formulas used in much more detail and with nice pictures. I recommend visiting their website if you want to learn more.

Schematic overview

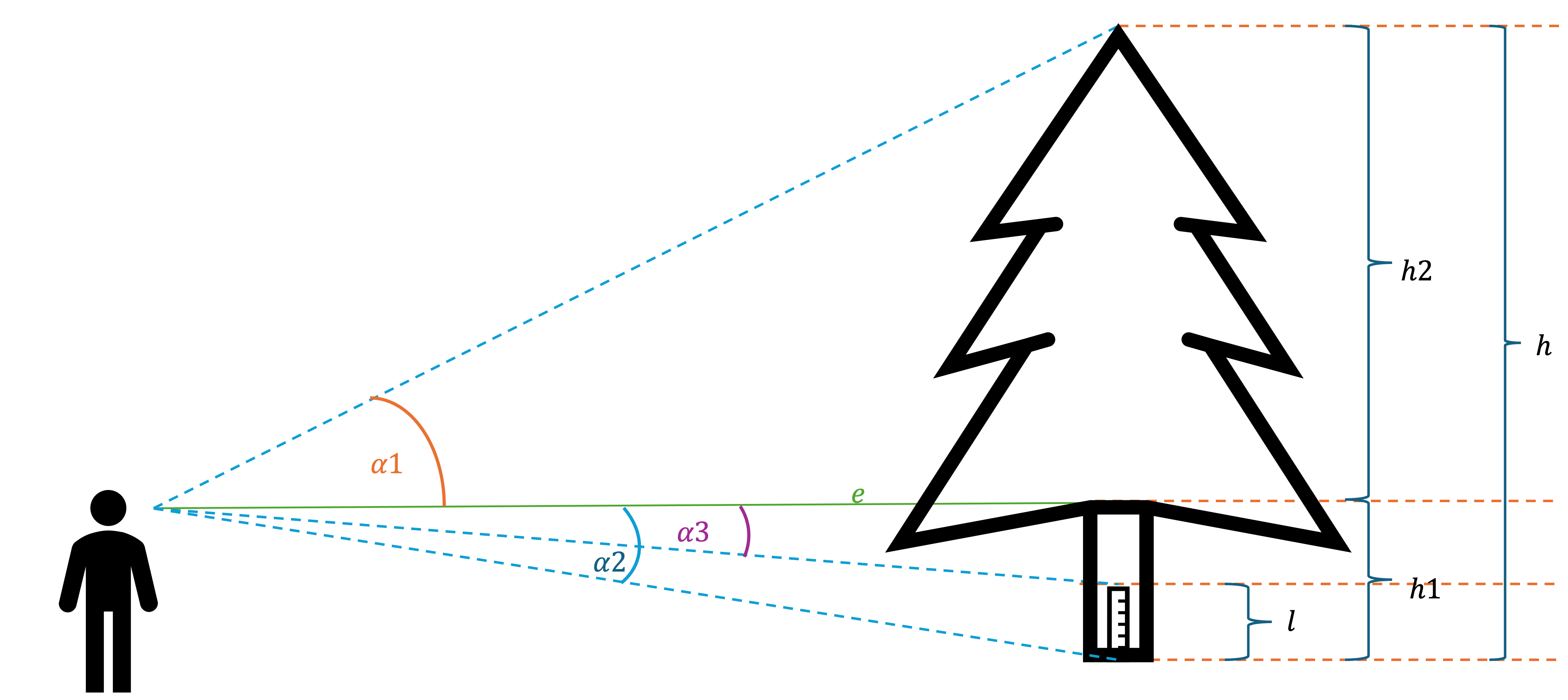
Definitions for the calculation

First, let's define some variables for the calculations.

• l: reference height in meters
• e: distance to the tree in meters
• \alpha1: angle between horizontal line and top of tree,
• \alpha2: angle between horizontal line and bottom of tree,
• \alpha3: angle between horizontal line and top of reference height

Formulas and Calculations

The reference height l can be calulated like this:

l = e * (tan (\alpha 3) - tan(\alpha 2))

By transforming the formula, the distance to the tree can be caculated like so:

e = \frac{l}{tan (\alpha 3) - tan(\alpha 2)}

Next, we can calculate the tree height. The tree height h is constructed of

• h1: distance between horizontal line and the top of the tree
• h2: distance between horizontal line and the bottom of the tree

and can be calculated as such:

h = h1 - h2

where h2 has to be multiplied by -1 if the bottom of the tree is below the horizontal line. Where this is done exactly is desribed further down in the additional considerations.

Next, we can use these formulas to get h1 and h2:

h1 = e * tan(\alpha1)

h2 = e * tan(\alpha2)

which leads to

h = e * tan(\alpha1) - (e * tan(\alpha2)) = e * (tan(\alpha1) - tan(\alpha2))

Thus, with the formula for e, we get the following final formula for calculating the tree height with a given reference height.

h = \frac{l}{tan (\alpha 3) - tan(\alpha 2)} * (tan(\alpha1) - tan(\alpha2))

Additional considerations

To get correct results, the following things have additonally been implemented.

Corrections for displaying angles in degrees

When using the integrated motion sensors, the iPhone measures angles in radians. For display, degrees are more usual and easier to grasp. The horizontal line is displayed as 90° in this app, as this is the orientation of the phone in relation to the horizontal line.

When converting radians to degrees for display, they will "repeat" when looking down or up (as they are the "difference" to the horizontal line and do not reflect the actual position of the angle within a circle).

This is why we must determine, if we are actually looking "up" or "down" (using the gravity "z" angle of the motion sensor) and apply a transformation.

This was done like this:

a) First, convert radians to degrees:

\alpha1(deg)=alpha1(rad) * \frac{180}{\pi}

b) next, if we are looking "up", transform it to be the correct angle:

\alpha1(deg) = 180 - alpha1(deg)

Angle corrections to correct observer standpoint

Depending on whether the measured angles are "positive" or "negative" - are looking "up" or "down" below the horizontal line - the angles have to be multiplied with -1. In the real world, this is the correction needed if the tree is located "uphill" or "downhill" from the observers standpoint.

By doing this transformation, the formula h = h1 - h2 always delivers correct results if the tree is completely above or below the observers standpoint.

When the iPhone is hold in portrait orientation, the horizontal line, in degrees, is 90°. In radian measurements from the motion sensor, all values above 90° are to be interpreted as "negative" and below 90° as "positive", so the formula for h keeps delivering the correct results.

So if looking "up", we multiply the angle with -1, if looking down, we keep the original radian value. This way we can keep the original height formula unchanged, as we already applied the necessary transformation at the angle part of the formulas.

Angle corrections for other cases

Depending on whether certain angles are above or below the horizontal line, there can be negative values for h. The case left after our previous transformations is when one measurement is above the horizontal line and one measurement is below it. This case would still lead to negative results for h, while the absolute value is correct. That is why abs is used to get the absolute value.

This way the same formula from above can be used, even if the tree is partly above and partly below the observers standpoint.